Statistics Tip of the Week: the F and Chi-Square Tests of Variance

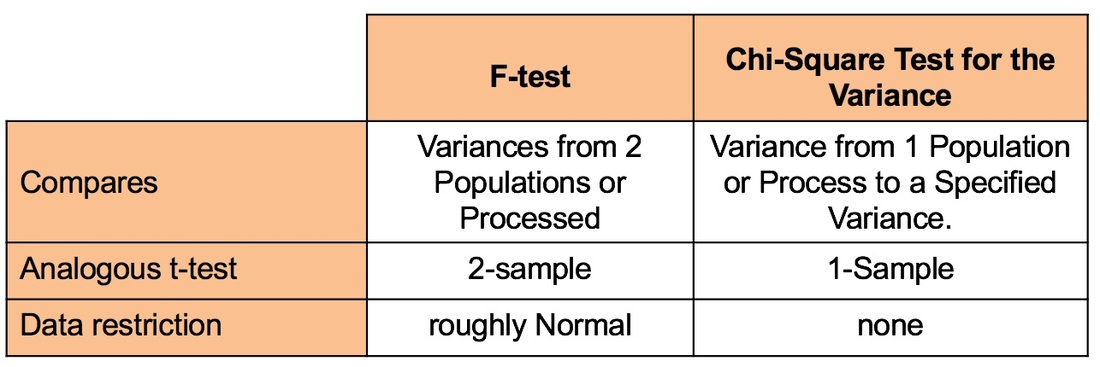
​Most users of Statistics are familiar with the F-test for Variances. But there is also a Chi-Square Test for the Variance. What's the difference?

The F-Test compares the Variances from 2 different Populations or Processes. It basically divides one Variance by the other and uses the appropriate F Distribution to determine whether there is a Statistically Significant difference.
 
If you're familiar with t-tests, the F-test is analogous to the 2-Sample t-test.
 
The F-test is a Parametric test. That is, it requires that the data from both the 2 Samples each be roughly Normal.
 
Chi-Square (like z, t, and F) is a Test Statistic. That is, it has an associated family of Probability Distributions.
 
The Chi-Square Test for the Variance compares the Variance from a Single Population or Process to a Variance that we specify. That could be a target value, a historical value, or anything else.
 
Since there is only 1 Sample of data from the single Population or Process, the Chi-Square test is analogous to the 1-Sample t-test.
 
The Chi-Square test is Nonparametric. It has no restrictions on the data.