|
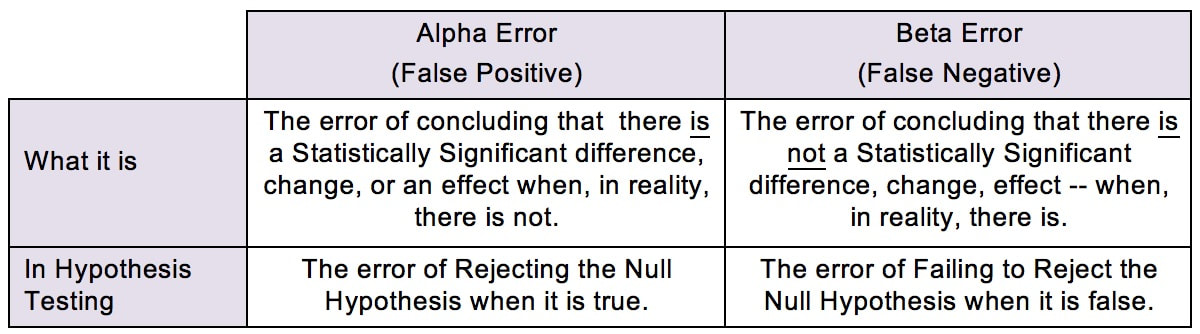
There are a number of see-saws (aka "teeter-totters" or "totterboards") like this in statistics. Here, we see that, as the Probability of an Alpha Error goes down, the Probability of a Beta Error goes up. Likewise, as the Probability of an Alpha Error goes up, the Probability of a Beta Error goes down. This being statistics, it would not be confusing enough if there were just one name for a concept. So, you may know Alpha and Beta Errors by different names:
The see-saw effect is important when we are selecting a value for Alpha (α) as part of a Hypothesis test. Most commonly, α = 0.05 is selected. This gives us a 1 – 0.05 = 0.95 (95%) Probability of avoiding an Alpha Error.
Since the person performing the test is the one who gets to select the value for Alpha, why don't we always select α = 0.000001 or something like that? The answer is, selecting a low value for Alpha comes at price. Reducing the risk of an Alpha Error increases the risk of a Beta Error, and vice versa. There is an article in the book devoted to further comparing and contrasting these two types of errors. Some time in the future, I hope to get around to adding a video on the subject. (Currently working on a playlist of videos about Regression.) See the videos page of this website for the latest status of videos completed and planned.
0 Comments
I just uploaded a new video. It's on Covariance, and it is the first in a playlist on Regression.
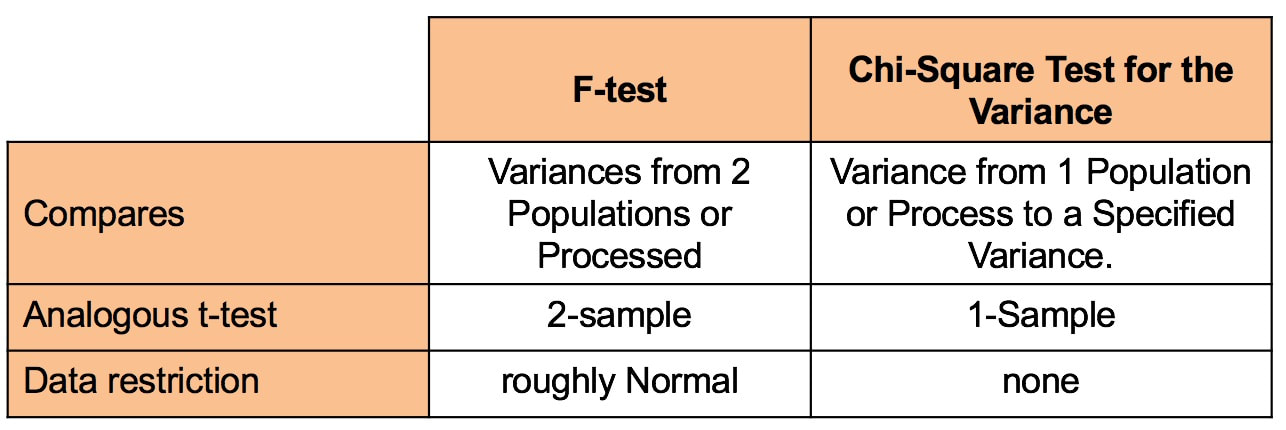
Most users of statistics are familiar with the F-test for Variances. But there is also a Chi-Square Test for the Variance. What's the difference? The F-test compares the Variances from 2 different Populations or Processes. It basically divides one Variance by the other and uses the appropriate F Distribution to determine whether there is a Statistically Significant difference. If you're familiar with t-tests, the F-test is analogous to the 2-Sample t-test. The F-test is a Parametric test. It requires that the data from both the 2 Samples each be roughly Normal. The following compare-and-contrast table may help clarify these concepts: Chi-Square (like z, t, and F) is a Test Statistic. That is, it has an associated family of Probability Distributions.
The Chi-Square Test for the Variance compares the Variance from a Single Population or Process to a Variance that we specify. That specified Variance could be a target value, a historical value, or anything else. Since there is only 1 Sample of data from the single Population or Process, the Chi-Square test is analogous to the 1-Sample t-test. In contrast to the the F-test, the Chi-Square test is Nonparametric. It has no restrictions on the data. Videos: I have published the following relevant videos on my YouTube channel, "Statistics from A to Z"
|
AuthorAndrew A. (Andy) Jawlik is the author of the book, Statistics from A to Z -- Confusing Concepts Clarified, published by Wiley. Archives
March 2021
Categories |



 RSS Feed
RSS Feed