|
David Leonhardt is an Op-Ed columnist for the New York Times. In his Christmas Eve column, he writes about probabilities. He is in favor of using them to communicate, but says, "They are inherently hard to grasp."
And, as we know, statistics is based on probabilities -- which is why so many find it confusing.
0 Comments
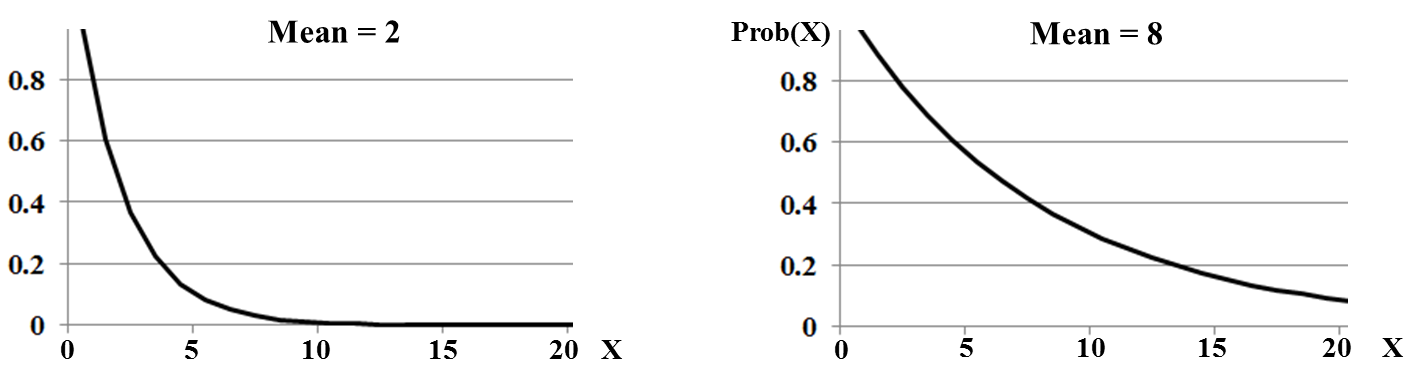
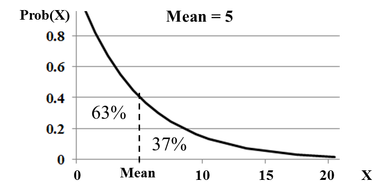
Continuing to add videos on Distributions to the YouTube channel for the book. The latest is on the Exponential Distribution. This is the 9th in the playlist on Distributions. The Videos page of this website has the latest status on videos.
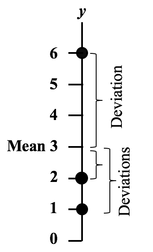
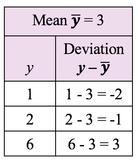
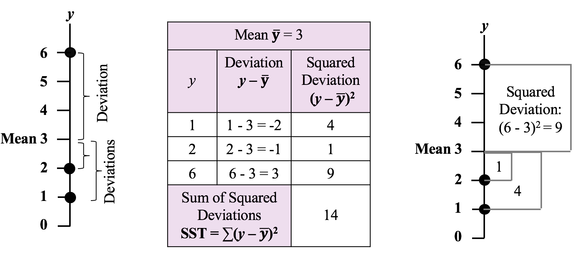
Many of the most common statistical analyses have fairly stringent "Assumptions". These are requirements that must be met if the analysis is to be valid. The most common Assumption is that the Population or Process data must have Parameters which approximate those of Normal Distributions like these: Parameters are statistical properties of a Population or Process, like the Mean or Standard Deviation. (Corresponding properties of Samples are called Statistics.) The key Parameters which define a Parametric (approximately Normal) Distribution are:
Parametric Assumption: Equal Variance Parametric methods which use 2 or more Samples from 2 different Populations or Processes usually assume roughly equal Variance. Nonparametric methods don't. Nonparametric methods can work with these: Nonparametric methods are often called "distribution-free", because they are free of any assumptions about the source Distribution(s).
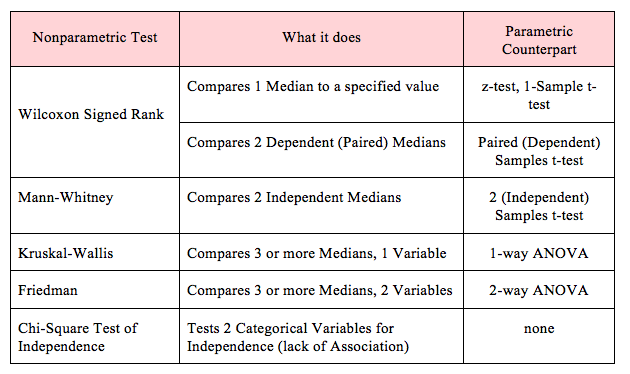
Here are some commonly-used Nonparametric tests and their Parametric Counterparts: "Reject the Null Hypothesis" is one of two possible outcomes of a Hypothesis Test. The other is "Fail to Reject the Null Hypothesis". Both of these statements can be confusing to many people. Let's try to clarify the concept of "Reject the Null Hypothesis". The Null Hypothesis states that there is no (Statistically Significant)
For example,
If the results of a statistical test indicate "Reject the Null Hypothesis", that means that we conclude that there is a (Statistically Significant)
What is the Null Hypothesis to which she is referring? As we said earlier, the Null Hypothesis says there is no difference, change, or effect. Before his proposal, they were not engaged to be married. So, if there is to be no difference, change, or effect in their relationship as a result of his proposal and her response, the Null Hypothesis would say that they are not to be engaged. But she rejects the Null Hypothesis. This indicates that she does want there to be a difference, change, or effect. She does want to change their status to engaged to be married.
If you still find this a little confusing, you might want to go to my YouTube channel and see the video on this subject: Reject the Null Hypothesis. There are also videos on these related concepts:
For more on available and planned videos based on content from my book, see the Videos page on this website. |
AuthorAndrew A. (Andy) Jawlik is the author of the book, Statistics from A to Z -- Confusing Concepts Clarified, published by Wiley. Archives
March 2021
Categories |












 RSS Feed
RSS Feed