Statistics Tip of the Week: Nonparametric tests and their Parametric counterparts

​Many of the most common statistical analyses have fairly stringent "Assumptions". These are requirements that must be met if the analysis is to be valid. The most common Assumption is that the Population or Process data must have Parameters which approximate those of Normal Distributions like these: 

Parameters are statistical properties of a Population or Process, like the Mean or Standard Deviation. (Corresponding properties of Samples are called Statistics.) The key Parameters which define a Parametric (approximately Normal) Distribution are:

• Mean = Mode = Median
• Skewness = 0 (the shape is Symmetrical)

Parametric Assumption: Equal Variance

Parametric methods which use 2 or more Samples from 2 different Populations or Processes usually assume roughly equal Variance. Nonparametric methods don't.

Nonparametric methods can work with these:

​Nonparametric methods are often called "distribution-free", because they are free of any assumptions about the source Distribution(s).
 
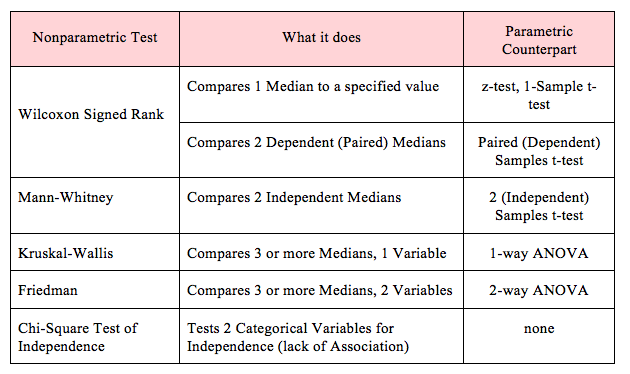
Here are some commonly-used Nonparametric tests and their Parametric Counterparts: