|
2 Comments
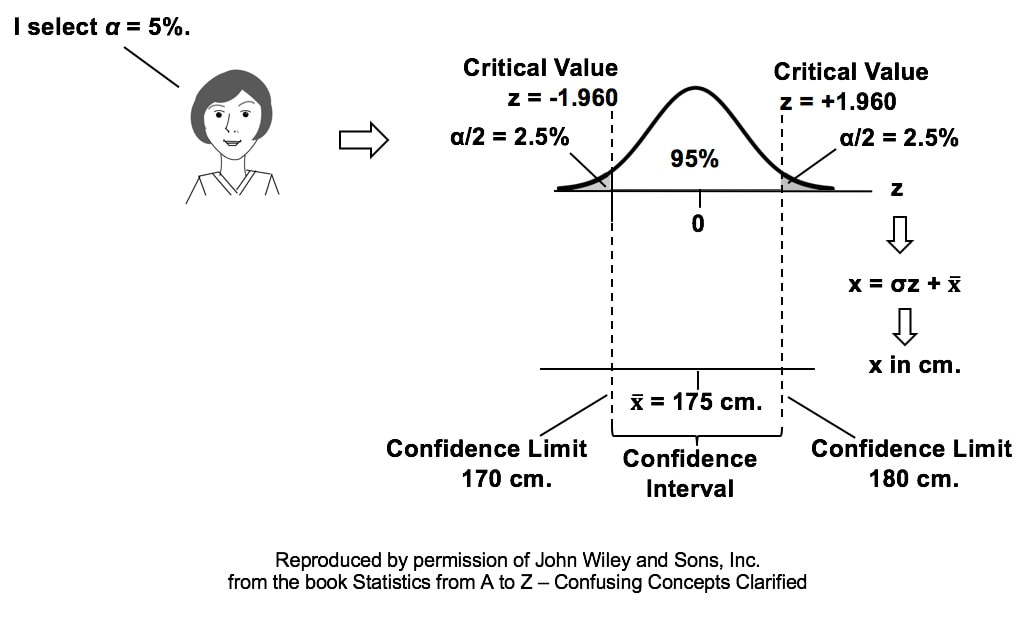
In our November 17, 2016 Tip of the Week, we showed how the concept of Alpha leads to the concept of Critical Value. This Tip shows how that, in turn, leads to the Critical Value.
This may be a handy table to keep around somewhere. How big a Sample Size do we need if we want to differentiate between 2 choices in a survey or election? It's more than people usually think.
Some might have in mind the guidance on when to use the t Distribution instead of the z (Standard Normal) Distribution. We're told we can use z when n, the Sample Size, is "large". And then we learn that some consider 30 to be large enough, while others say 100. But as you can see from this table, n = 100 barely gets you into the game when you're doing a survey or poll. When n = 100, you have a 10% Margin of Error (MOE). That is, you can say that you have a Statistically Significant difference if your Proportions are wider spread than 44% and 55% for the 2 candidates. But to get to a 2% MOE, you'd need a Sample Size of 2,400. Notice also, that diminishing returns set in. To get to a 1% MOE, you'd need a sample 4 times larger than you would for 2%. This Thursday, 6 - 7:15, I'll be speaking at the Greenwich library, 101 West Putnam Avenue, Greenwich CT. Hope to see you there.
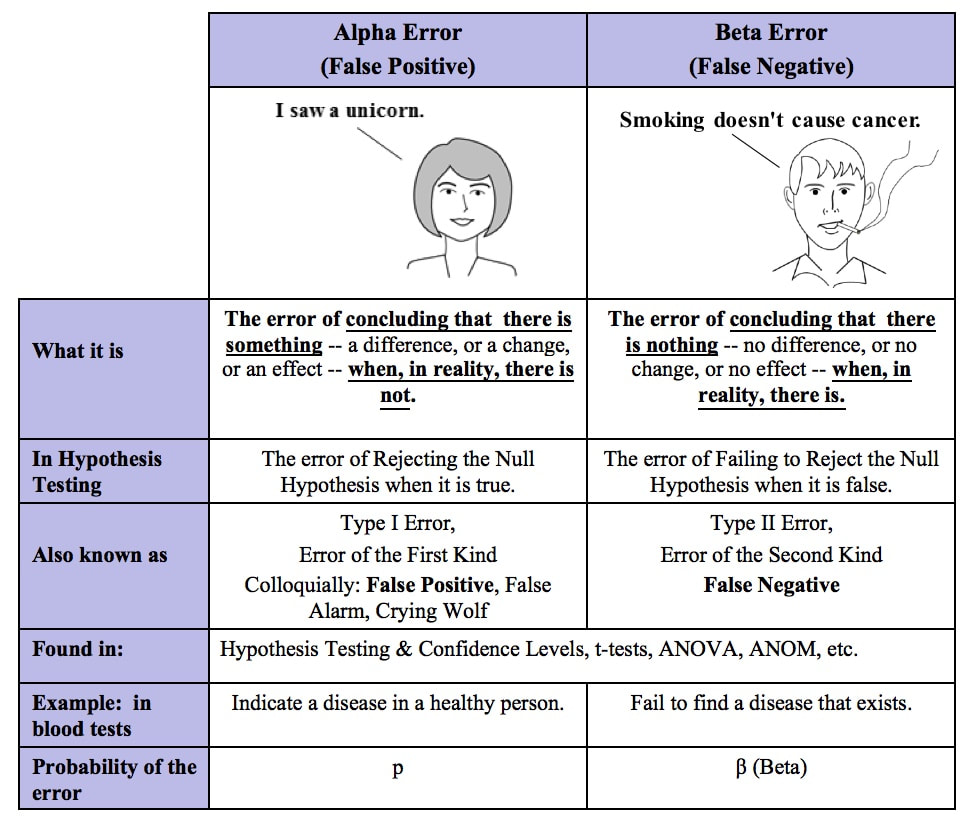
In Hypothesis Testing, "Fail to Reject the Null Hypothesis" is one of two possible conclusions to be drawn from the test. The other is "Reject the Null Hypothesis." We are all taught in elementary school to avoid using double negatives, like "I don't have no money." However, statistics goes beyond the double negative to an even more confusing triple negative: "Fail to Reject the Null Hypothesis." Fail, Reject, and Null are all negative words This is like saying, "I don't not have no money." That statement confuses a lot of people. It may help to understand better if we represent a positive statement by +1 and a negative by -1. In Hypothesis Testing, we are usually trying to determine whether there is a Statistically Significant difference, change, or effect. For more on how to clarify this confusing concept, please see my video, Fail to Reject the Null Hypothesis. It has received very good reviews, like these:
|
AuthorAndrew A. (Andy) Jawlik is the author of the book, Statistics from A to Z -- Confusing Concepts Clarified, published by Wiley. Archives
March 2021
Categories |







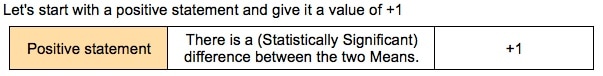



 RSS Feed
RSS Feed