|
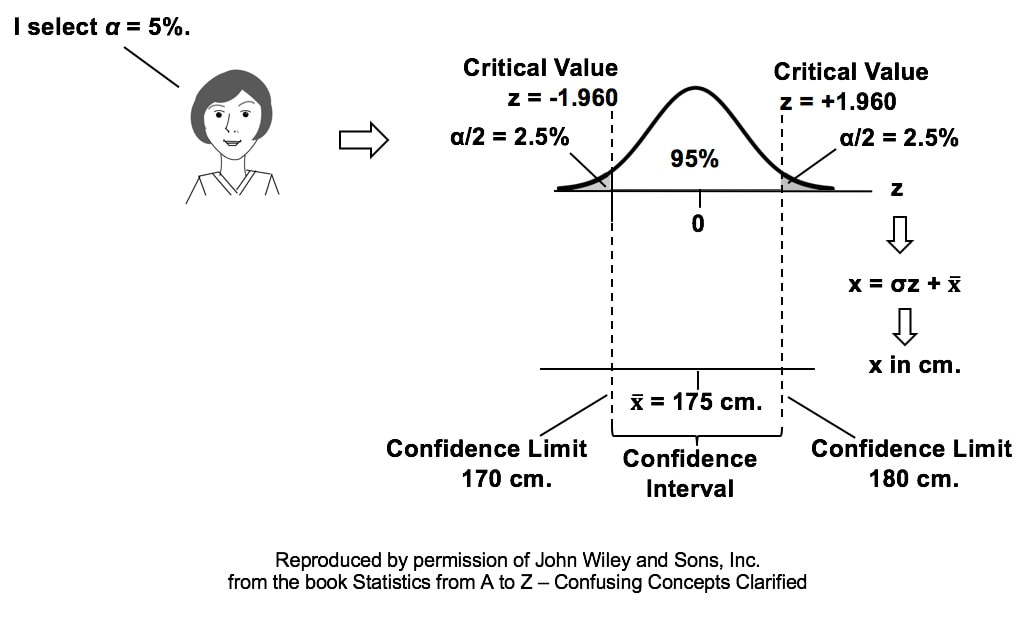
In our November 17, 2016 Tip of the Week, we showed how the concept of Alpha leads to the concept of Critical Value. This Tip shows how that, in turn, leads to the Critical Value.
0 Comments
Leave a Reply. |
AuthorAndrew A. (Andy) Jawlik is the author of the book, Statistics from A to Z -- Confusing Concepts Clarified, published by Wiley. Archives
March 2021
Categories |

 RSS Feed
RSS Feed