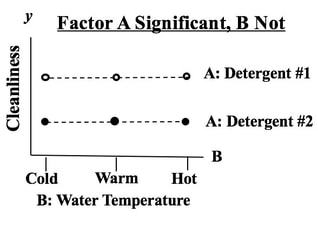
Statistics Tip: In 2-Factor (2-Way) ANOVA, separated lines show that Factor A has an effect10/24/2019 In this example, we are testing 2 Factors for their effect on the y Variable, Cleanliness.
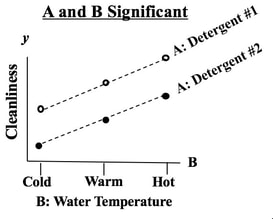
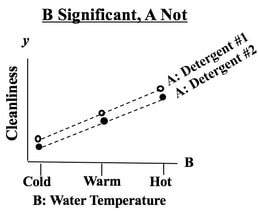
We see from the graph that -- for all three levels of Factor B, Detergent #1 cleans better than Detergent #2. The lines are substantially separated, indicating that the difference is Statistically Significant. (The ANOVA numbers will tell us for sure.) If Factor B did have an effect, the lines would be slanted. Again, separated lines tell us that Factor A has an effect. If the lines were not separated, as below, then Factor A does not have an effect.
0 Comments
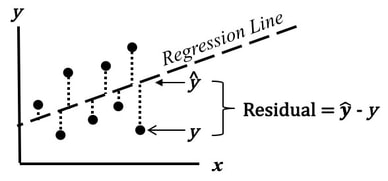
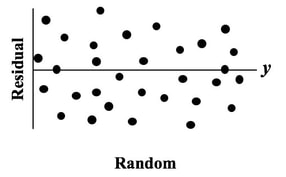
The purpose of Regression analysis is to develop a cause and effect "Model" in the form of an equation. To keep things simple, let's talk about Simple Linear Regression, in which the equation is y = bx + a The Regression analysis comes up with the values for b and a. Residuals represent the Error in the Regression Model. They represent the Variation in the y variable which is not explainedby the Regression Model. So, Residuals must be Random. If not -- if Residuals form a pattern -- that is evidence that one or more additional factors (x's) influence y. A Scatterplot of Residuals against y-values should illustrate Randomness: Being Random means that the Residuals
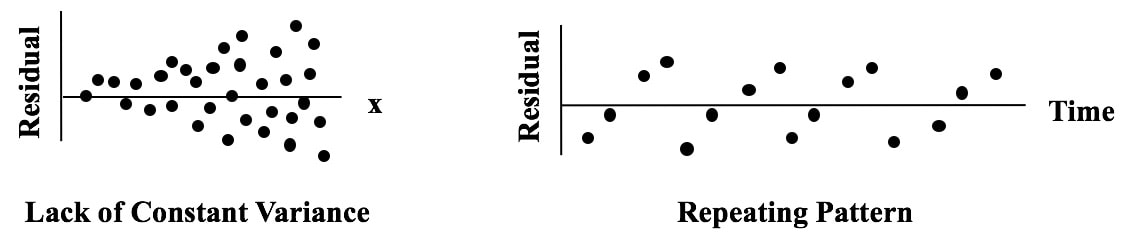
Here are some patterns which indicate the Regression Model is incomplete. |
AuthorAndrew A. (Andy) Jawlik is the author of the book, Statistics from A to Z -- Confusing Concepts Clarified, published by Wiley. Archives
March 2021
Categories |

 RSS Feed
RSS Feed