Statistics Tip: Don't extrapolate your conclusions beyond the range of your data.

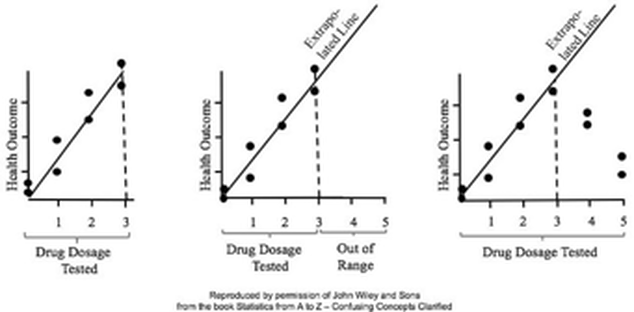
​In Regression, we attempt to fit a line or curve to the data. Let's say we're doing Simple Linear Regression in which we are trying to fit a straight line to a set of (x,y) data.

We test a number of subjects with dosages from 0 to 3 pills. And we find a straight line relationship,  y = 3x, between the number of pills (x) and a measure of health  of the subjects. So, we can say this.

But we cannot make a statement like the following:

​This is called extrapolating  the conclusions of your Regression Model beyond the range of the data used to create it. There is no mathematical basis for doing that, and it can have negative consequences, as this little cartoon from my book illustrates.

​In the graphs below, the dots are data points. In the graph on the left, it is clear that there is a linear correlation between the drug dosage (x) and the health outcome (y) for the range we tested, 0 to 3 pills. And we can interpolate between the measured points. For example, we might reasonably expect that 1.5 pills would yield a health outcome halfway between that of 1 pill and 2 pills.

 For more on this and other aspects of Regression, you can see the YouTube videos in my playlist on Regression.  (See my channel: Statistics from A to Z - Confusing Concepts Clarified.