Statistics Tip of the Week, 01/25/2018: In ANOVA, the Sum of Squares Within (SSW) is the sum of the variations within each of several groups.

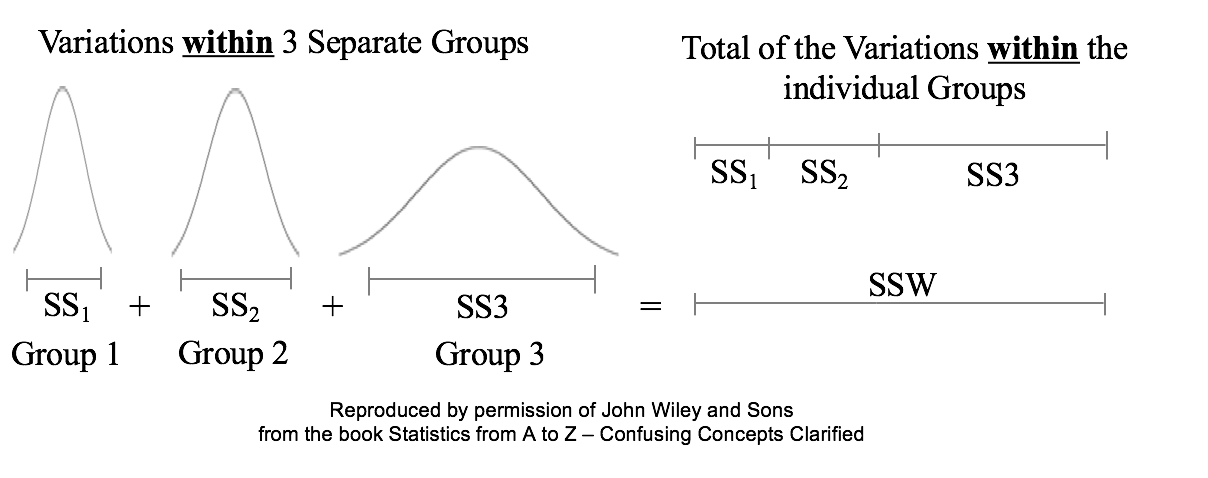
Sums of Squares are measures of variation; there are a number of different types. Our Tip of the Week for Dec. 21, 2017 described Sum of Squares Total (SST), which is used in Regression.  Sum of Squares Within (SSW) is used in ANOVA.  Sum of Squares Between (SSB) is also used in ANOVA, and it will be the topic of another Statistics Tip of the Week.
 
Sum of Squares Within, SSW, is the sum of the Variations (as expressed by the Sums of Squares, SS's) within each of several Groups (usually Samples).

SSW = SS1 + SS2  + ... + SSn

​This is not numerically precise, but conceptually, one might picture SS as the width of the "meaty" part of a Distribution curve – the part without the skinny tails on either side.

​Sums of Squares Within, SSW, summarizes how much Variation there is within each of the Groups– by giving the sum of all such Variations.

​A comparatively small SSW indicates that the data within the individual Groups are tightly clustered about their respective Means. If the data in each Group represents the effects of a particular treatment, for example, this is indicative of consistent results (good or bad) within each individual treatment. "Small" is a relative term, so the word "comparatively" is key here. We'll need to compare SSW with SSB before being able to make a final determination.                                                                            
 
A comparatively large SSW shows that the data within the individual Groups are widely dispersed. This would indicate inconsistent results within each individual treatment. 

For more on the subject and related concepts see my video, ANOVA Part 2 (of 4): How it Does It.