Statistics Tip of the Week: A comparison of various measures of Variation

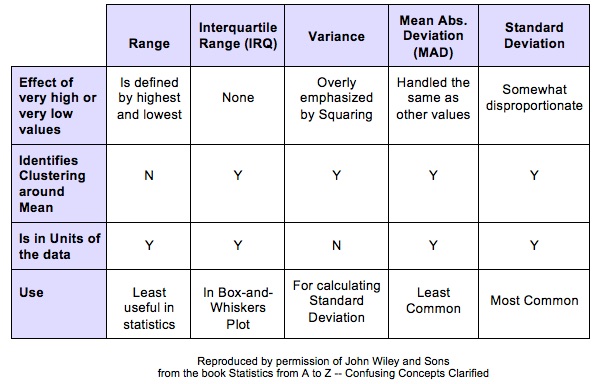
Variation is also known as "Variability", "Dispersion", "Spread", and "Scatter". (5 names for one thing is one more example why statistics is confusing.) Variation is 1 of 3 major categories of measures describing a Distribution or data set. The others are Center (aka "Central Tendency") with measures like Mean, Mode, and Median and Shape (with measures like Skew and Kurtosis). Variation measures how "spread out" the data is.

There are a number of different measures of Variation. This compare-and-contrast table shows the relative merits of each.

---

• The Range is probably the least useful in statistics. It just tells you the highest and lowest values of a data set, and nothing about what's in between.
• The Interquartile Range (IQR) can be quite useful for visualizing the distribution of the data and for comparing several data sets -- as described in my recent blog post.
• Variance is the square of the Standard Deviation, and it is used as an interim step in the calculation of the latter. This squaring emphasizes the effects of very high or very low values. Another drawback is that it is in units of the data squared, which can be meaningless (e.g. square kilograms). There is a Chi-Square Test for the Variance, and Variances are used in F-tests and in the calculations in ANOVA.
• The Mean Absolute Deviation is the average (unsquared) distance of the data points from the Mean. It is used when it is desirable to avoid overly emphasizing the effects of high and low values 
• The Standard Deviation, being the square root of the Variance, does not overly emphasize the high and low values as the Variance does. Another major benefit is that it is in the same units as the data.