Statistics Tip of the Week: Analyze the Residuals in Your Regression Model

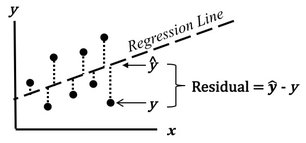
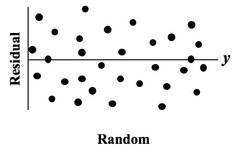
The purpose of Regression analysis is to develop a cause and effect "Model" in the form of an equation. To keep things simple, let's talk about Simple Linear Regression, in which the equation is y = bx + a. The Regression analysis comes up with the values for b and a.

​Residuals represent the Error in the Regression Model. They represent the Variation in the y variable which is not explained by the Regression Model. 

​So, Residuals must be Random.  If not -- if Residuals form a pattern -- that is evidence that one or more additional Factors (x's) influence y.
 
A Scatterplot of Residuals against y-values should illustrate Randomness: 

Being Random means that the Residuals

• are Normally distributed, 
• have constant Variance, 
• show no patterns when graphed, 
• and have no unexplained Outliers.

 
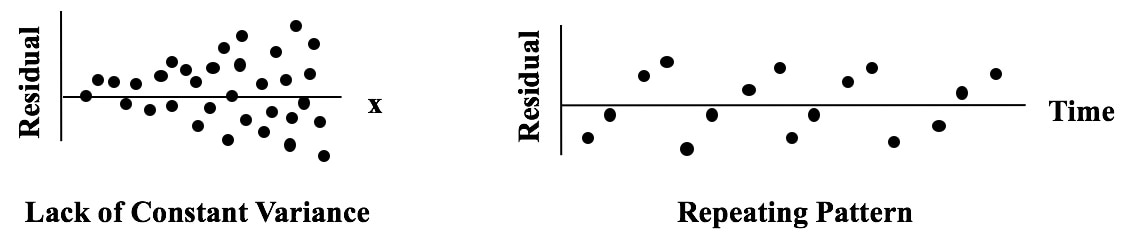
Here are a couple of patterns which indicate the Regression Model is incomplete.