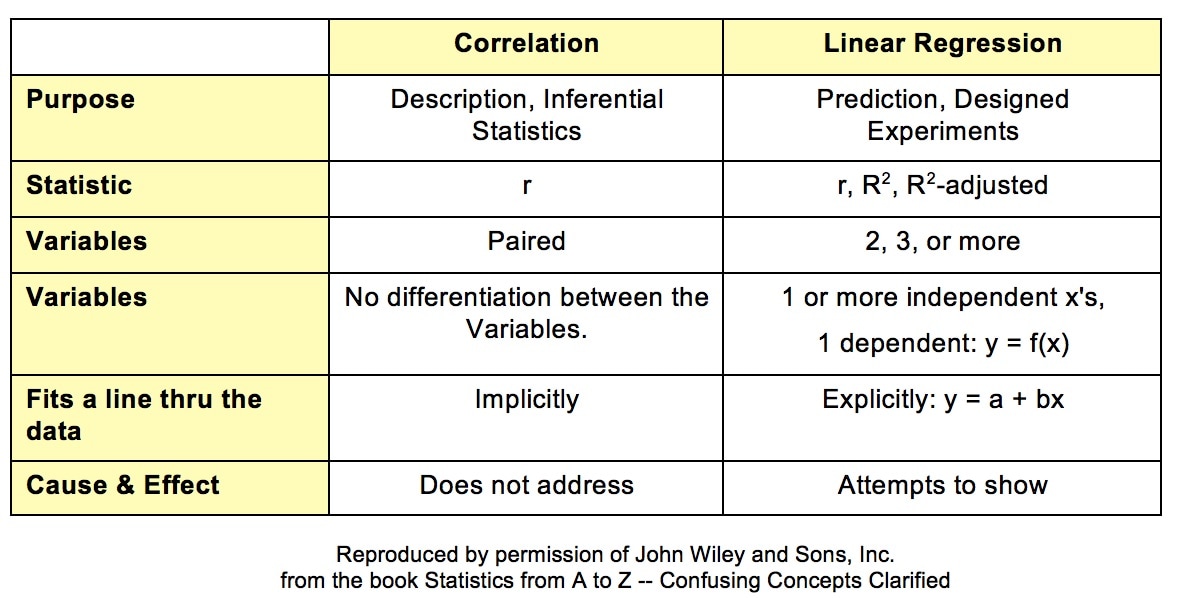
Statistics Tip of the Week: Establishing Correlation is a Prerequisite for Linear Regression

​Establishing Correlation is a prerequisite for Linear Regression.
 
We can't use Linear Regression unless there is a Linear Correlation. The following compare-and-contrast table may help in understanding both concepts.

Correlation analysis describes the present or past situation. It uses Sample data to infer a property of the source Population or Process. There is no looking into the future. The purpose of Linear Regression, on the other hand, is to define a Model (a linear equation) which can be used to predict the results of Designed Experiments.

Correlation mainly uses the Correlation Coefficient, r. Regression also uses r, but employs a variety of other Statistics.

Correlation analysis and Linear Regression both attempt to determine whether 2 Variables vary in synch. Linear Correlation is limited to 2 Variables, which can be plotted on a 2-dimensional x-y graph. Linear Regression can go to 3 or more Variables/ dimensions.

In Correlation, we ask to what degree the plotted data forms a shape that seems to follow an imaginary line that would go through it. But we don't try to specify that line. In Linear Regression, that line is the whole point. We calculate a best-fit line through the data: y = a + bx.

Correlation Analysis does not attempt to identify a Cause-Effect relationship, Regression does.