|
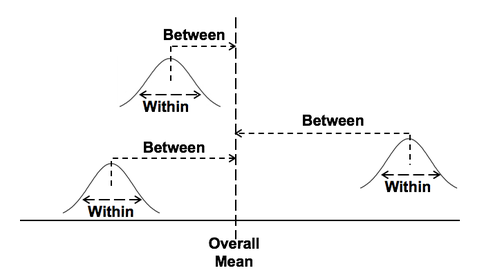
In our Tip of the Week for Jan 25, 2018, we described Sum of Squares Within (SSW) as a measure of Variation in a group (sample, population or process) of data values. In ANOVA, Sum of Squares Between (SSB) is used together with SSW to determine whether there is a Statistically Significant difference among the Means of several groups. Here's a conceptual illustration of Variation Within and Between groups. Each bell-shaped curve represents a group. The widths of the curves represent how much variation there is within each. That is what SSW represents. For the variation between Means, we calculate the differences between the Means of each group and the Overall Mean. Then, we square those differences and then we sum those squares. This gives us the Sum of Squares Between, SSB. where X-bar is the Mean of an individual group and x-double-bar is the Overall Mean.
ANOVA then calculates a Mean SSB (MSB) and a Mean SSW (MSW). The previous Tip of the Week describes how these are used to calculate the value of the Test Statistic F in the F-test which produces the conclusion from the ANOVA. There is also more on this in my YouTube Video ANOVA-- Part 2, How It Does It.
1 Comment
|
AuthorAndrew A. (Andy) Jawlik is the author of the book, Statistics from A to Z -- Confusing Concepts Clarified, published by Wiley. Archives
March 2021
Categories |

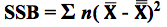
 RSS Feed
RSS Feed