|
The Binomial Distribution is used with Count data. It displays the Probabilities of Count data from Binomial Experiments. In a Binomial Experiment,
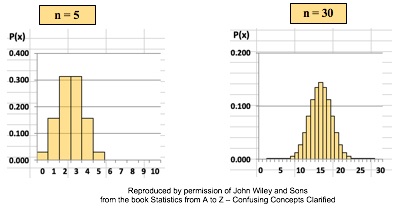
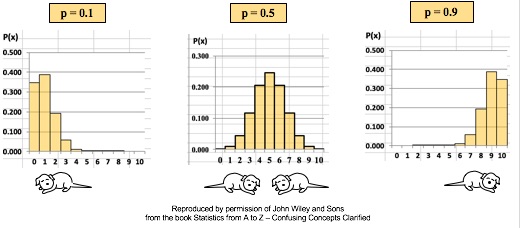
There are many Binomial Distributions. Each one is defined by a pair of values for two Parameters, n and p. n is the number of trials, and p is the Probability of each trial. The graphs below show the effect of varying n, while keeping the Probability the same at 50%. The Distribution retains its shape as n varies. But obviously, the Mean gets larger. The effect of varying the Probability, p, is more dramatic. For small values of p, the bulk of the Distribution is heavier on the left. However, as described in my blog post of October 4, statistics describes this as being skewed to the right, that is, having a positive skew. (The skew is in the direction of the long tail.) For large values of p, the skew is to the left, because the bulk of the Distribution is on the right.
0 Comments
Leave a Reply. |
AuthorAndrew A. (Andy) Jawlik is the author of the book, Statistics from A to Z -- Confusing Concepts Clarified, published by Wiley. Archives
March 2021
Categories |

 RSS Feed
RSS Feed