Statistics Tip of the Week: The p-value is calculated as the area under the curve bounded by the Test Statistic value

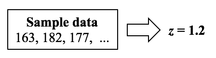
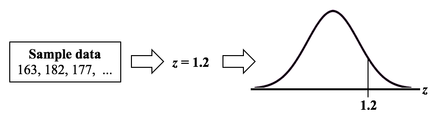
​p is the Probability of an Alpha (false positive) Error. The p-value is calculated as the area under the curve bounded by the Test Statistic value.  

As shown in the concept flow diagram above, the first thing we do is take the Sample data and calculate a value for the Test Statistic.  In this example, the value of the Test Statistic, z, is calculated to be 1.2.

​​Next, (illustrated here for a 1-tailed test), we plot the Test Statistic value on the horizontal axis of the Probability Distribution of the Test Statistic.  (For a 2-tailed test, we would plot 1/2 the value of z at the left and right ends sides of the curve. In this example, we would plot z/2 = 0.6 and -z/2 = -0.6).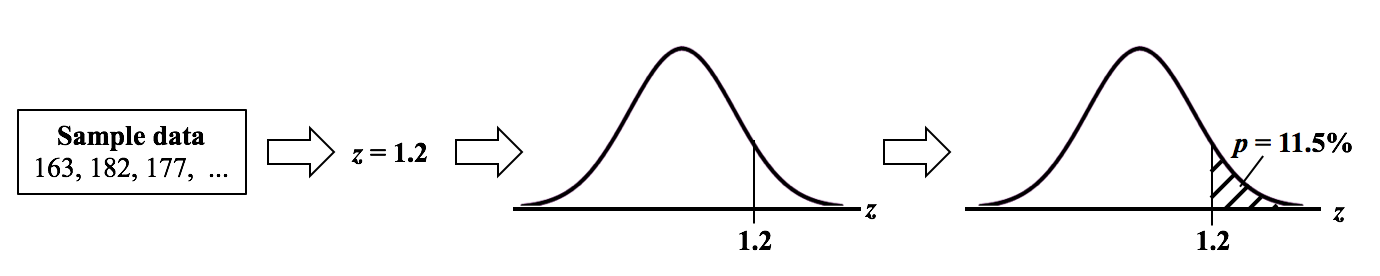

The Test Statistic Value forms the boundary of an area under the curve extending outward from the Test Statistic value. Here we show a hatched area from z = 1.2 outward to infinity.
 
The hatched area under the curve is calculated as the Cumulative Probability of all points under the curve from z = 1.2 outward. This gives us the value for p.

---

For more on the concepts involved here, please see my videos:

• Test Statistic  https://youtu.be/2fz0STTfIIU
• p, the p-value https://youtu.be/vyX4m89VkyI
• Alpha, p, Critical Value and Test Statistic: How they work together. https://youtu.be/SAYGehjRZ8E