Statistics Tip of the Week: The values in a Sampling Distribution are not data but Statistics of Samples.

The concept of Sampling Distribution may not be used so much used on its own as it is used in describing the concepts of the Central Limit Theorem and Standard Error:

• Central Limit Theorem: Even if the data are not Normally distributed, the Sampling Distribution of the Means or Proportions of the data approaches the Normal Distribution as the Sample Size, n, increases.
• The Standard Error is defined as the Standard Deviation of the Sampling Distribution.

In this Tip of the week, we're not going to go into those two concepts any further; we'll just focus on Sampling Distribution.
 
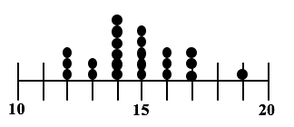
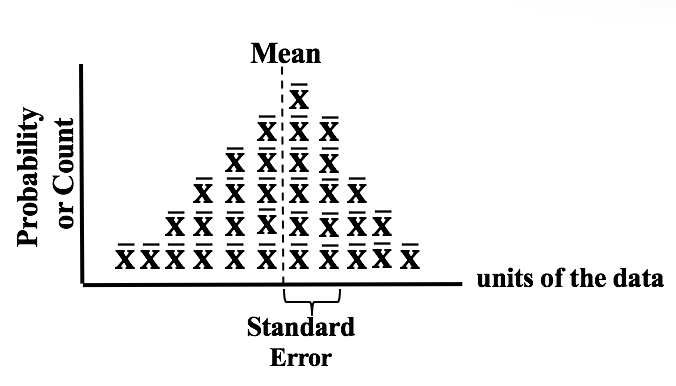
The visual we're going to use is similar to a Dot Plot of a Sample of data. Each dot represents a single value of x in the Sample. In the example below, 6 values in the Sample were x = 14, so we show 6 dots over "14" on the horizontal x-axis.

​In a Sampling Distribution, the values which are plotted are not individual data points as in this dot plot. The values are Statistics calculated from Samples. Statistics are numerical properties of Samples, such as the Mean or Proportion or Standard Deviation. Let's show a plot of the Means of some Samples of data. Instead of a dot, we'll show each Mean as an x-bar symbol.

The x-bars are stacked vertically above the x axis at the point which represents their value. The height of each stack corresponds to the Probability of that value of the Mean.
​
This illustration shows a Sampling Distribution. The Sampling Distribution would show the Means of every possible Sample of a given size, n.
 
You can see that the x-bars form a shape which roughly resembles a Normal Distribution. If we had many more Samples with a large n, the resemblance would be much closer. And if we calculate the Standard Deviation of the Distribution, we would get the Standard Error of the Mean.