Statistics Tip: p < Alpha is the same as Test Statistic > Critical Value

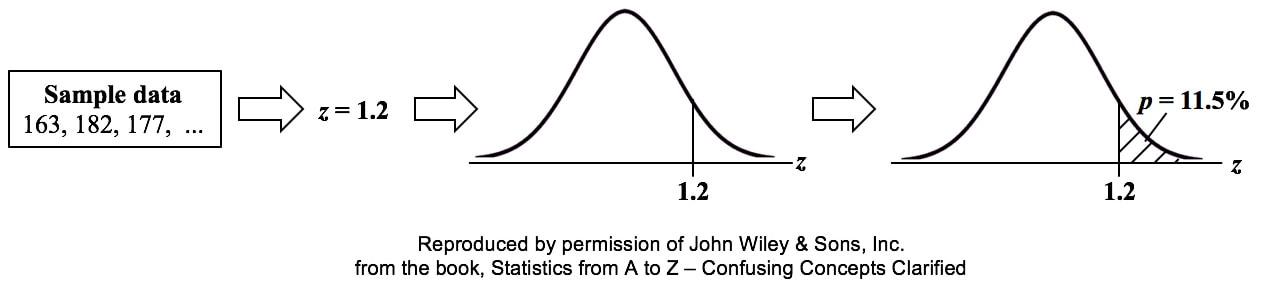
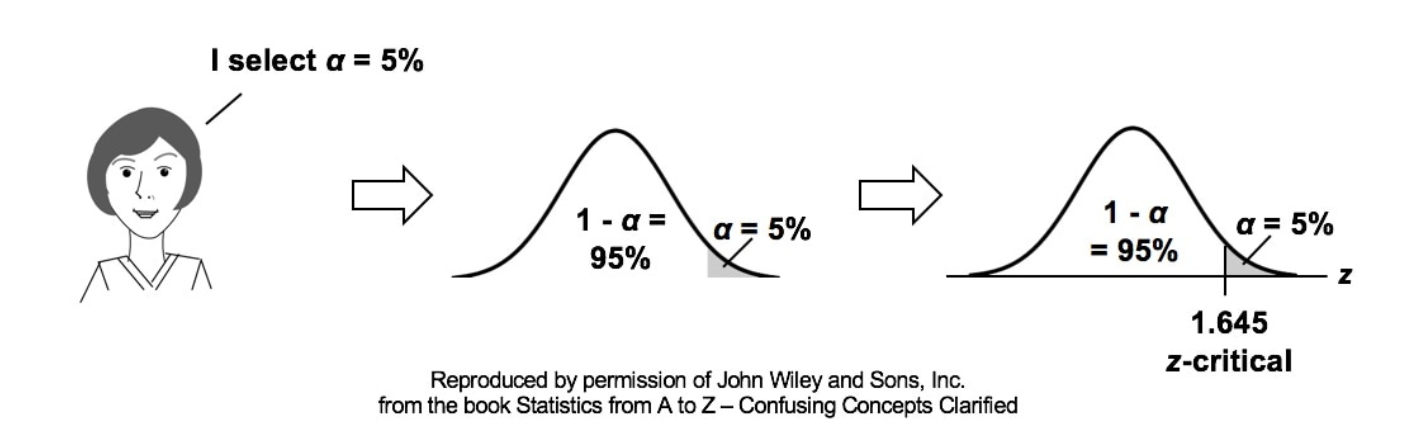
p is the Probability of an Alpha (False Positive) Error. Alpha (α) is the Level of Significance; its value is selected by the person performing the statistical test. If p < α (some say if p < α) then we Reje​ct the Null Hypothesis. That is, we conclude that any difference, change, or effect observed in the Sample data is Statistically Significant. 

The p-value contains the same information as the Test Statistic Value, say z. That is because the value of z is used to determine the p-value. As shown in the following concept flow diagram,

1. Sample data is used to calculate a value for a Test Statistic, say, z.
2. This value of z forms the boundary for the area under the curve which represents the Cumulative Probability, p.
3. From this, tables or calculations give us the value of p.

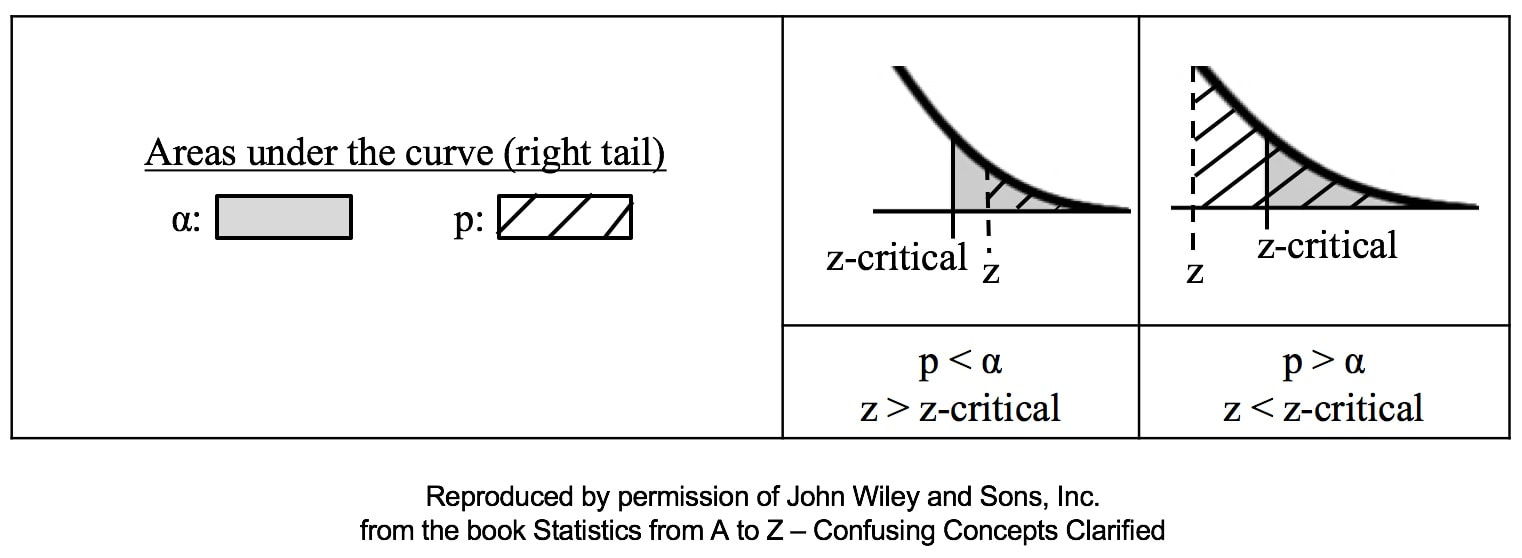
​Similarly α contains the same information as the Critical Value. 

So comparing p and the Critical Value is the same as comparing Alpha and the Test Statistic value. But the comparison symbols ( ">" and  "<") point in the opposite direction. That's because p and Test Statistic have an inverse relation. A smaller value for p means that the Test Statistic value must be larger.

See also the videos for

• p, the p-value​
• Alpha (α), the Significance Level
• Null Hypothesis
• Reject the Null Hypothesis
• Critical Value
• Test Statistic