Statistics Tip: Statistics See-saws: Test Statistic and p-value

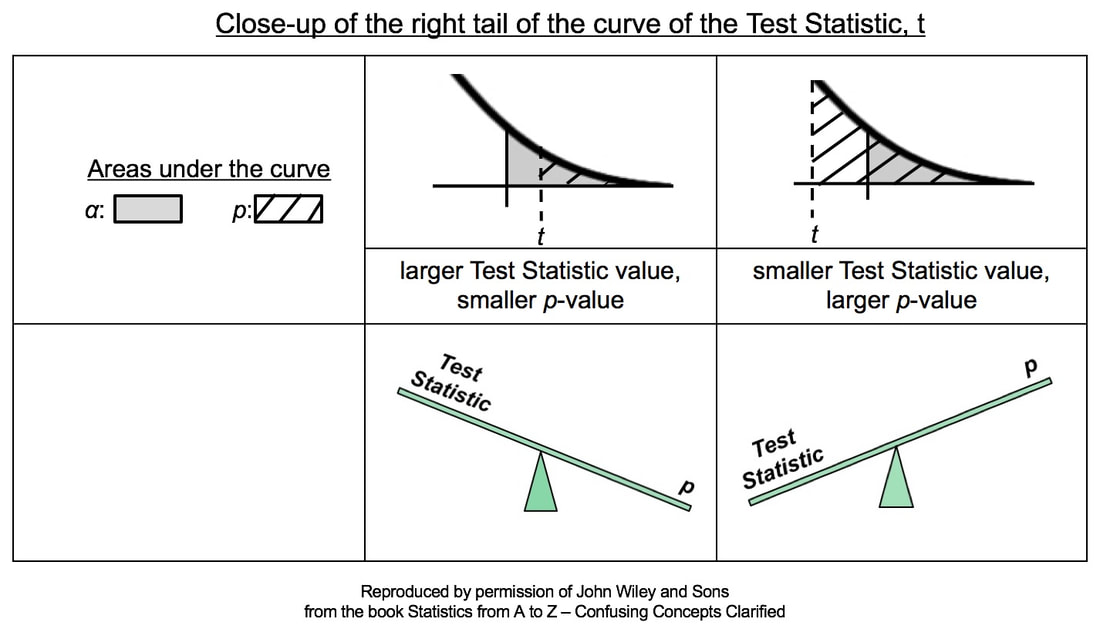
A larger Test Statistic value (such as that for z, t, F, or Chi-Square) results in a smaller p-value. The p-value is the Probability of an Alpha (False Positive) Error.
 
​And conversely, a smaller Test Statistic value results in a larger value for p.
 
Here's how it works:

• A value of the Test Statistic, say t, is calculated from the Sample data.
• That value is plotted on the horizontal axis of the Distribution of the Test Statistic.
• p is then calculated as the area under the curve bounded by the Test Statistic value. It is shown as the hatched area in the diagrams below.

​In the close-ups of the right tail, zero is not visible. It is the center of the bell-shaped t curve, and it is out of the picture to the left. So, a larger value of the Test Statistic, t, would be farther to the right. And, the hatched area under the curve representing the p-value would be smaller. This is illustrated in the middle column of the table above.
 
Conversely, if the Test Statistic is smaller, then it's value is plotted more to the left, closer to zero. And so, the hatched area under the curve representing p would be larger. This is shown in the rightmost column of the table.